Simplified Tutorial for New Users
Here you will find a concise and straightforward guide to downloading, installing, and running the Einstein Toolkit. For a more detailed tutorial, view the Tutorial for New Users.
Prerequisites
You will need a number of packages installed in order to download the Einstein Toolkit components, and if you follow the instructions in this tutorial. On a Debian, Linux-Mint or Fedora-based system, install them as follows:
# Debian (squeeze) su apt-get install build-essential g++ gfortran libopenmpi-dev openmpi-bin git subversion curl gnuplot # Mint13 (likely Ubuntu oneiric ocelot as well) sudo apt-get install libopenmpi-dev openmpi-bin gfortran g++ git subversion curl gnuplot # Fedora (incomplete) yum install git wget
Downloading
A script called GetComponents is used to fetch the components of the Einstein Toolkit. GetComponents serves as convenient wrapper around lower level tools like git and svn to download the codes that make up the Einstein toolkit from their individual repositories. You may download and make it executable it as follows:
curl -O https://raw.github.com/gridaphobe/CRL/ET_2012_05/GetComponents chmod a+x GetComponents
GetComponents accepts a thorn list as an argument. To check out the needed components:
./GetComponents --parallel https://svn.einsteintoolkit.org/manifest/branches/ET_2012_05/einsteintoolkit.th
which downloads the master thorn list from the Einstein toolkit server and proceeds to download all thorns.
This thornlist checks out Cactus, the Einstein Toolkit, and Simulation Factory.
Configuring
You may proceed to configure Simfactory which requires some changes for some OS.
cd Cactus # for Mint13 (mpich2 needs mpl so we add it to the MPI_LIBS line using sed) sed '/MPI_LIBS/s/mpich/mpich mpl/' <simfactory/mdb/optionlists/debian.cfg >simfactory/mdb/optionlists/mint.cfg ./simfactory/bin/sim setup --optionlist=mint.cfg # for Debian ./simfactory/bin/sim setup --optionlist=debian.cfg # for Fedora ./simfactory/bin/sim setup --optionlist=fedora.cfg
Accept the default values for all options.
Building
Now that you have configured Simfactory, you may build:
./simfactory/bin/sim build --thornlist=manifest/einsteintoolkit.th
This may take a while, as it compiles all the thorns specified in manifest/einsteintoolkit.th.
Running
The example files provided at for the most part too large to run on a single machine. You can try however to run the static_tov example which is smallest and requires about 1.3GB of RAM to run and will run for about 24 hours using a single core. To speed up the run, you can try and reduce the resolution by increasing the parameters "CoordBase::dx", "CoordBase::dy", and "CoordBase::dz" from 8 to 12 whic will reduce runtime to roughly 5 hours and memory consumption to 800MB.
sed '/CoordBase::d[xyz]/s/8/12/' <par/static_tov.par >par/static_tov_small.par ./simfactory/bin/sim submit static_tov --parfile=par/static_tov_small.par --procs=1 --walltime=8:0:0 ./simfactory/bin/sim show-output --follow static_tov
Look at Results
When the simulation is complete (ie. when "All done" appears in the output), stop simfactory by pressing CTRL-C and move to the output directory. The command should be:
cd ~/simulations/static_tov/output-0000/static_tov
You should see a number of files with the extenstion .asc. These are 0-D (reductions of 3-D grid functions to scalar values) and 1-D ASCII output files that can be plotted with gnuplot.
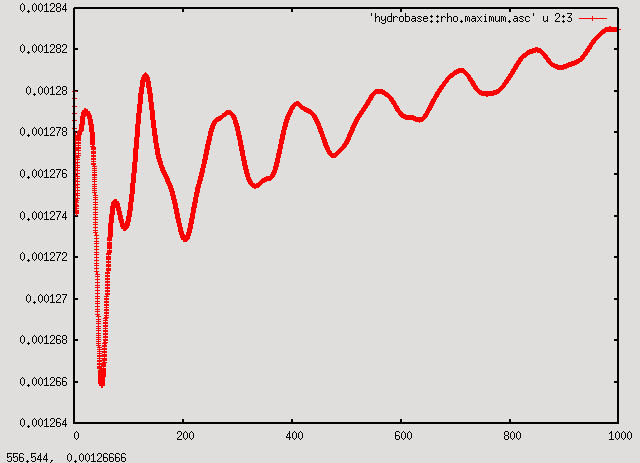
In this case it's interesting to look at the maximum of the density (in the file hydrobase::rho.maximum.asc). Start gnuplot with the command:
gnuplot
and at the gnuplot prompt type:
plot 'hydrobase::rho.maximum.asc' using 2:3 with linespoints
This plots the data in column 3 (rho) as a function of the data in column 2 (time).
As can be seen from the plot, the maximum of the density oscillates with decreasing amplitude around the initial value with a small drift upwards. Even though the initial model is supposed to be in equilibrium, numerical errors means that the numerical model is not exactly in equilibrium and it starts to oscillate. The oscillation energy is slowly dissipated by shocks, decreasing the oscillation amplitude, while the star contracts in response, increasing the maximum density.
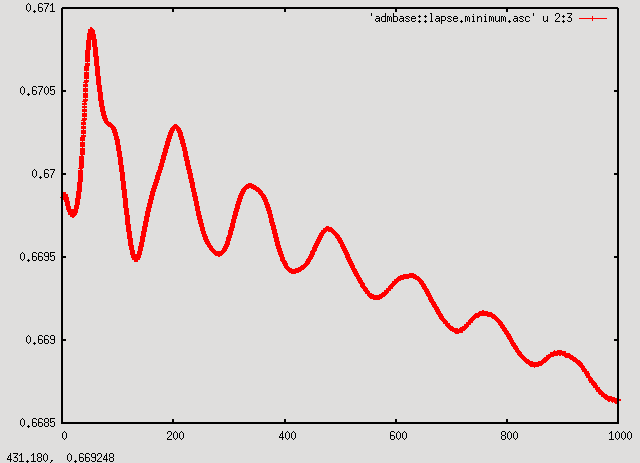
A consistent picture can be seen by plotting the minimum of the lapse:
p 'admbase::lapse.minimum.asc' u 2:3 w lp
The quantity shows the same features as the maximum of the density, except the drift is downwards. The downwards trend stems from the contraction of the star. As the star contracts, the curvature of spacetime increases slightly. In response, the singularity avoiding lapse condition used here decreases the lapse.
As the oscillations and subsequent drift of the density and the lapse are caused by numerical error, increasing the numerical resolution will decrease these effects.